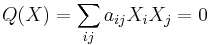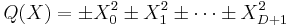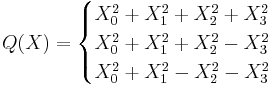Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in (D + 1)-dimensional space defined as the locus of zeros of a quadratic polynomial. In coordinates {x1, x2, ..., xD+1}, the general quadric is defined by the algebraic equation[1]
which may be compactly written in vector and matrix notation as:
where x = {x1, x2, ..., xD+1} is a row vector, xT is the transpose of x (a column vector), Q is a (D + 1)×(D + 1) matrix and P is a (D + 1)-dimensional row vector and R a scalar constant. The values Q, P and R are often taken to be real numbers or complex numbers, but in fact, a quadric may be defined over any ring. In general, the locus of zeros of a set of polynomials is known as an algebraic variety, and is studied in the branch of algebraic geometry.
A quadric is thus an example of an algebraic variety. For the projective theory see quadric (projective geometry).
Contents |
Euclidean plane and space
Quadrics in the Euclidean plane are those of dimension D = 1, which is to say that they are curves. Such quadrics are the same as conic sections, and are typically known as conics rather than quadrics.
In Euclidean space, quadrics have dimension D = 2, and are known as quadric surfaces. By making a suitable Euclidean change of variables, any quadric in Euclidean space can be put into a certain normal form by choosing as the coordinate directions the principal axes of the quadric. In three-dimensional Euclidean space there are 16 such normal forms. Of these 16 forms, five are nondegenerate, and the remaining are degenerate forms. Degenerate forms include planes, lines, points or even no points at all.[2]
| Non-degenerate real quadric surfaces | ||
|---|---|---|
| Ellipsoid | 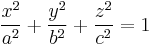 |
|
| Spheroid (special case of ellipsoid) | 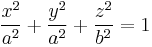 |
|
| Sphere (special case of spheroid) | 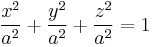 |
|
| Elliptic paraboloid | 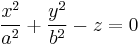 |
|
| Circular paraboloid (special case of elliptic paraboloid) | 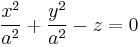 |
|
| Hyperbolic paraboloid | 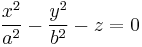 |
|
| Hyperboloid of one sheet | 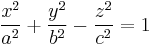 |
|
| Hyperboloid of two sheets | 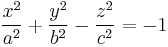 |
|
| Degenerate quadric surfaces | ||
| Cone | 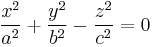 |
|
| Circular Cone (special case of cone) | 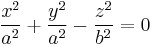 |
|
| Elliptic cylinder | 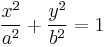 |
|
| Circular cylinder (special case of elliptic cylinder) | 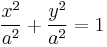 |
|
| Hyperbolic cylinder | 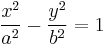 |
|
| Parabolic cylinder | 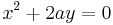 |
|
Projective geometry
The quadrics can be treated in a uniform manner by introducing homogeneous coordinates on a Euclidean space, thus effectively regarding it as a projective space. Thus if the original (affine) coordinates on RD+1 are
one introduces new coordinates on RD+2
related to the original coordinates by 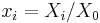 . In the new variables, every quadric is defined by an equation of the form
. In the new variables, every quadric is defined by an equation of the form
where the coefficients aij are symmetric in i and j. Regarding Q(X) = 0 as an equation in projective space exhibits the quadric as a projective algebraic variety. The quadric is said to be non-degenerate if the quadratic form is non-singular; equivalently, if the matrix (aij) is invertible.
In real projective space, by Sylvester's law of inertia, a non-singular quadratic form Q(X) may be put into the normal form
by means of a suitable projective transformation. The normal forms of singular quadrics can have zeros as well as ±1 for coefficients. This normal form thus classifies real non-singular quadrics up to a projective transformation. In dimension D = 2, there are exactly three inequivalent cases:
Consequently, the ellipsoid, the elliptic paraboloid and the hyperboloid of two sheets are equivalent to each other up to a projective transformation as these all correspond to the second normal form. The hyperbolic paraboloid and the hyperboloid of one sheet are both equivalent to the third form (these are ruled surfaces). The cone and the cylinder are equivalent to the degenerate form
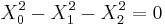 .
.
These latter are degenerate quadrics because the coefficient on X3 is zero; they also have zero Gaussian curvature.
In complex projective space all of the nondegenerate quadrics become indistinguishable from each other.
See also
- Superquadrics
- Conic section
- Focus (geometry), an overview of properties of conic sections related to the foci.
- Quadratic function
- Klein quadric
References
- Iskovskikh, V.A. (2001), "Quadric", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=q/q076220
- Weisstein, Eric W., "Quadric" from MathWorld.
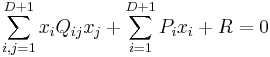
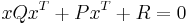
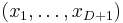
![[X_0,\dots,X_{D%2B1}]](/2012-wikipedia_en_all_nopic_01_2012/I/5cc7cebdd23e39bc8d7da065c70958a1.png)